Uma razão incrível!

Em matemática, o infinito é um número .

Ainda que seja p número mais estranho que conhecemos.

Usamos a palavra infinito para descrever algo que seja sem fim - in (prefixo de negação) e finito (fim) -,  sem limites e sem restrições.

O infinito é um conceito desconcertante para a mente, especialmente para nós, que vivemos em um universo fechado e finito, com um número finito de átomos. Alguns cientistas estimam que esse número seja da ordem de 1081 (1 seguido de 81 zeros), o que é menos que um googol - medida interessante e que vale apena pesquisar e descobrir a conexão como Google, por curiosidade digite esse nome no Google -.

O famoso "paradoxo do Grande Hotel", desenvolvido pelo matemático alemão David Hilbert (1862-1943) fornece um vislumbre do mundo estranho do infinito.

O hotel de Hilbert

O hotel de Hilbert tem um número infinito de quartos alinhados em um corredor infinito e numerados como 1, 2, 3, ... para sempre. Um noite, todos estavam ocupados; ainda assim, a placa de "vagas" ainda estava acesa. Um novo cliente chega e pede por um quarto. "Sem problemas", diz o esperto proprietário com um sorriso, e em seguida move o hóspede que ocupava o quarto 1, para o 2 o ocupante do 2 para o 3 e assim por diante. Ele, então, pede que o novo cliente use o quarto 1, que se torna vago assim que todos os clientes se acomodam em seus novos quartos.

O Hotel de Hilbert (Hilbert à esquerda). Extraído de: http://www.astropt.org/2015/05/06/paradoxos-da-razao-parte-iii/

Na noite seguinte, um ônibus de turistas, com um número infinito de turistas a bordo, chega ao hotel. "Sem problemas", exclama o proprietário e, diz: "Apenas espere um minuto". Com infinita paciência, ele move o hóspede do quarto 1 para o quarto 2, o hóspede do quarto 2 para o 4, o hóspede do quarto 3, para o 6, e assim por diante, deixando todos os quartos de números ímpares livres para o número infinito de novos hóspedes.

O hotel infinito nunca ficará sem quartos livres para um número infinito de ônibus de turistas, cada um cheio de um número infinito de turistas, se eles chegarem ao mesmo tempo. Em um mundo de infinitos, uma parte pode ser igual ao todo.

Um pouco de superstição e matemática: leminscata!

O astrofísico britânico, Arthur Eddington (1882-1944), não era fã do infinito: "Essa grande quantidade , o 'infinito' é um grande incômodo, e nenhum físico racional teria qualquer coisa a ver com isso. Talvez seja por isso que os matemáticos o representem com um sinal parecido com um laco amoroso".

O que Eddington chama de um laço amoroso é, na verdade, um 8 preguiçoso: os matemáticos o chamam de lemnsicata - mas calma, aí! Não é Lemniscata a nossa ex professora do ProIFPE, não ela exatamente ... -. O símbolo foi introduzido em 1655 por um matemático inglês chamado John Wallis (1616-1703). Ele o usava como um atalho, ainda usado em cálculo, para a expressão "tornando-se grande e positivo".

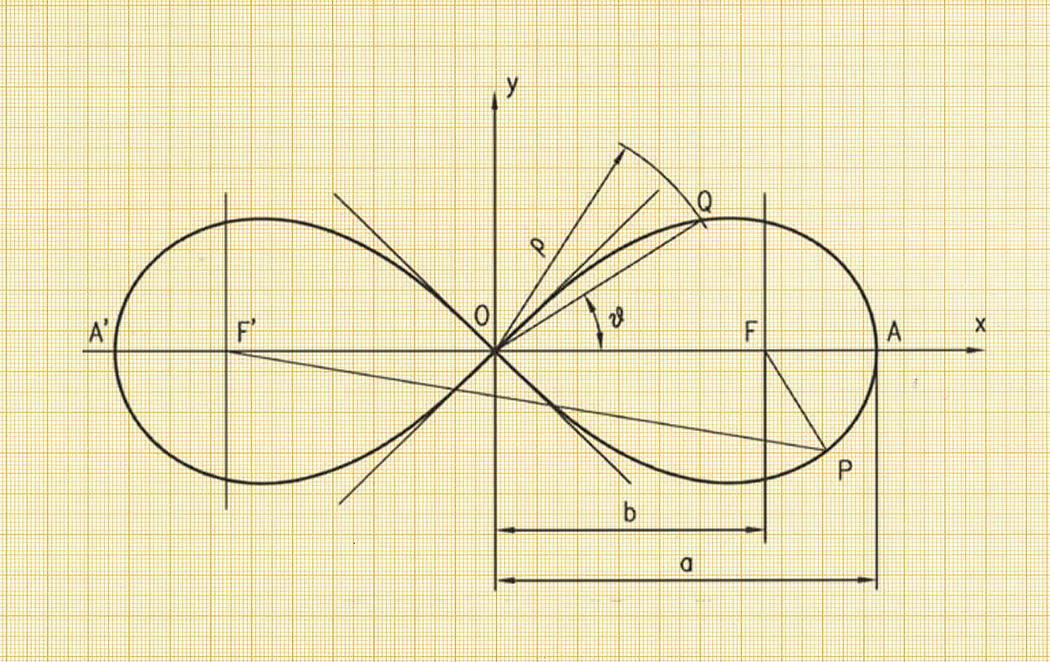Anatomia da lemniscata, extraído de: https://medium.com/@ysperanza/a-lemniscata-180f75dcd484

O jovem dessa rima clássica estava tão envolvido no laço amoroso do infinito que ele decidiu encontrar a raiz quadrada do infinito para impressionar a sua namorada:

 Era uma vez um jovem de Trinity

Que resolveu a rais quadrada de infinito

Ao contas os dígitos,

Ele se inquietou com os símbolos

Deixou a ciência e assumiu a

Divindade, decrépito

O paradoxo do infinito na Grécia antiga

Séculos antes, Zenão também se enfureceu com os números infintos ao descobrir seus famosos paradoxos, um deles a disputa de Aquiles e a Tartaruga.

Aquiles e a tartaruga:

O mais famoso dos paradoxos de Zenão, fiz que o mais rápido de dois corredores jamais poderá superar o outro, caso um deles possa começar primeiro que o outro. Dessa forma, Aquiles - um dos heróis da guerra de Tróia e da mitologia grega, famoso por ser um primoroso corredor - nunca alcançaria uma taruga se esta começasse primeiro. Digamos que a tartaruga tem uma vantagem inicial de 100 metros. Quando Aquiles, que é dez vezes mais rápido que a tartaruga, tiver corrido 100 metros, a tartaruga terá corrido outros 10 metros. Assim continuaria eternamente. Como Aquiles tem intervalos infinitos para percorrer, ele nunca poderia alcançar a tartaruga. 

E não se incomodou tentando resolver a raiz do infinito.

Aqui estão algumas estranhas propriedades de infinito (n é um número comum):

• n + ∞ = ∞
• n - ∞ = -∞
• n * ∞ = ∞ (se n não for igual a zero, se n for negativo n*∞= -∞);
• ∞/n =∞ (se n não for igual a zero, se n for negativo n/∞= -∞);
• n/∞= 0 (para n diferente de zero);
• n/0 = ∞ (caso n não seja negativo, ou igual a zero)/
• ∞+∞=∞
• ∞*∞=∞
• ∞*0, ∞-∞ e ∞, são respostas indeterminadas. Basicamente, operações não permitidas.

Texto extraído do livro: Ideias geniais na matemática, Surenda Verma.